dbnBIAL – aplikacja implementująca dynamiczną sieć bayesowską, opisującą progresję przewlekłej białaczki limfocytowe B-komórkowej, umożliwiająca przewidywanie, jak zmienia się stan zdrowia pacjenta na przestrzeni 25 lat od rozpoznania choroby z uwzględnieniem dostępnej wiedzy na temat danego pacjenta.
Opis & Grafika:
Opracowana aplikacja dbnBIAL implementuje dynamiczną sieć bayesowską, pozwalającą na przewidywanie zmian w czasie stanu zdrowia pacjentów chorych na przewlekłą białaczkę limfocytową B-komórkową.
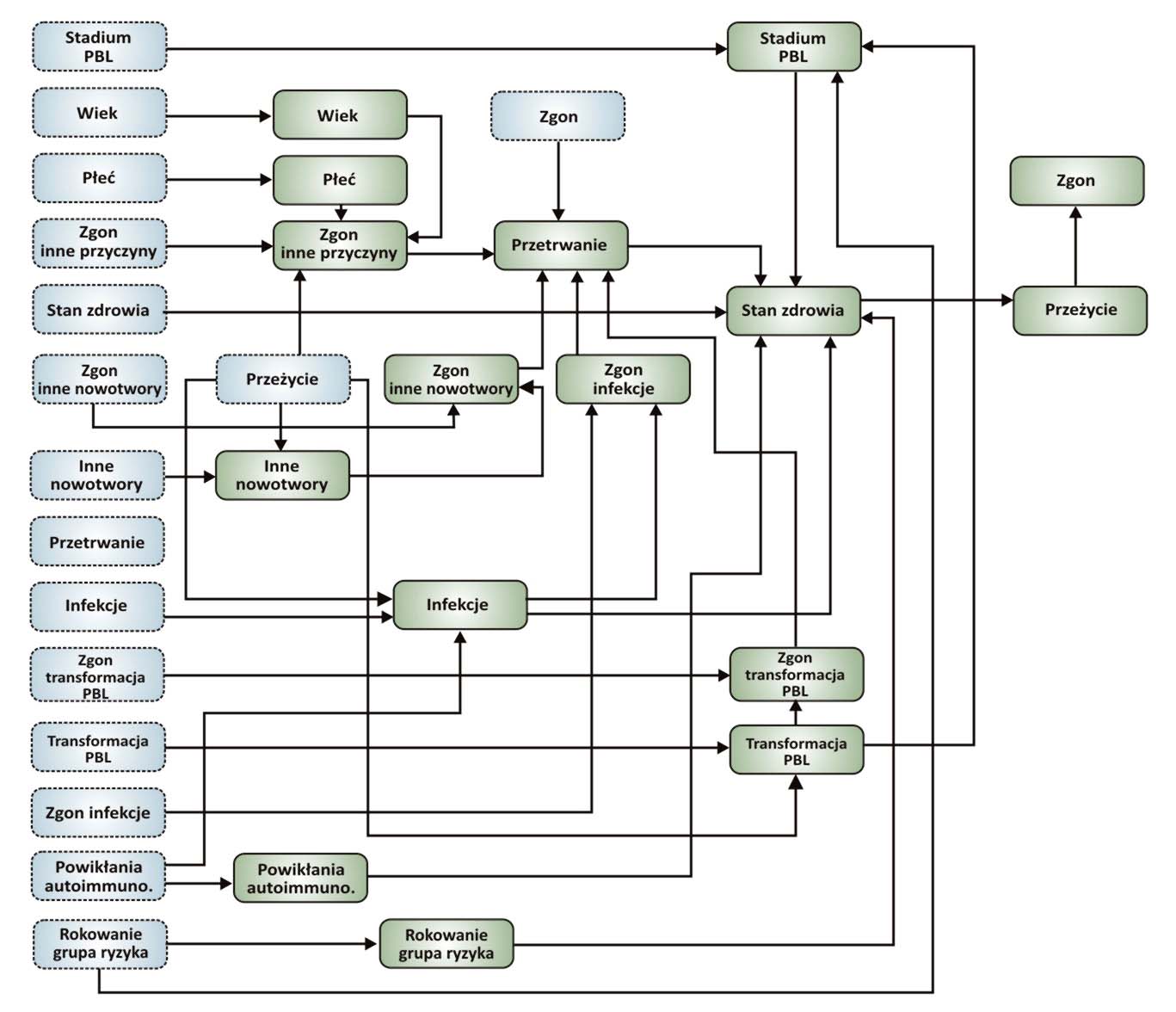
Schemat sieci zaimplementowanej w aplikacji dbnBIAL dla dwóch pierwszych chwil czasowych oddalonych od siebie o 6 miesięcy przedstawiono na poniższym rysunku.
Węzły oznaczone linią przerywaną i niebieskim tłem reprezentują stan sieci w chwili początkowej, tj. w chwili diagnozy a węzły oznaczone linią ciągłą i zielonym tłem – jej stan po 6 miesiącach. Tablice prawdopodobieństw warunkowych definiujące powiązania występujące pomiędzy zmiennymi stanowiącymi poszczególne węzły sieci określono na podstawie dostępnych danych literaturowych, wyników zgromadzonych w bazie danych systemu NetBIAL oraz wiedzy ekspertów medycznych współpracujących przy realizacji projektu. Zakłada się, że powiązania poszczególnych węzłów w kolejnych chwilach czasowych (odległych od siebie o 6 miesięcy) nie ulegają zmianie i w związku z tym określenie stanu sieci odbywa się poprzez „rozwinięcie” sieci na kolejne chwile czasowe.
Poniżej opisano poszczególne węzły opracowanej sieci.
Rokowanie, grupa ryzyka bazuje na parametrach, które decydują o tym, czy chory cierpi na postać progresywną PBL czy łagodną. W modelu przyjęto, że węzeł ten może przyjmować trzy wartości: dobre, średnie i złe. Rokowania są związane z czynnikami prognostycznymi, czyli głównie z zaburzeniami cytogenetycznymi, mutacją genu IgVH i wybranymi markerami immunofenotypowymi komórki białaczkowej (CD38, ZAP70). Przyjęto, że rokowania dobre występuje gdy pacjent nie ma aberracji cytogenetycznych lub tylko delecję 13q, mutację genu IgVH oraz prawidłowe wartości markerów immunofenotypowych. Rokowania średnie to zaburzenia cytogenetyczne: delecja 11q lub trisomia 12, brak mutacji genu IgVH. Złe rokowania to przede wszystkim zaburzenie cytogenetyczne 17p, które powoduje szybki rozwój PBL i zgon w ciągu liku lat od rozpoznania choroby [1,2], niezależnie od innych czynników prognostycznych i stadium PBL. Założono, że raz nabyte czynniki rokownicze nie ulegają zmianie w czasie. Dlatego prawdopodobieństwo dla tego węzła w kolejnych chwilach czasowych jest określone następująco (t – oznacza wartość w bieżącej a t-1 w poprzedniej chwili czasowej):
P(Rokowaniet = k | Rokowaniet-1 = k) = 1, gdzie kÎ{dobre, średnie, złe}
Kolejnym czynnikiem wpływającym na stan zdrowia pacjenta z PBL są Powikłania autoimmunologiczne, czyli małopłytkowość i niedokrwistość. Prawdopodobieństwo dla tego węzła jest określane następująco:
P(Powikłania autoimmunologicznet = tak | Powikłania autoimmunologicznet-1 = tak) = 1
P(Powikłania autoimmunologicznet = tak | Powikłania autoimmunologicznet-1 = nie) = x
Gdzie x oznacza wartość prawdopodobieństwa oszacowaną na podstawie aktualnego stanu wiedzy.
Transformacja PBL w agresywny nowotwór głównie syndrom Richtera występuje rzadko, tj. w ok. 5% przypadków [3]. Chorzy przeżywają średnio ok 3 lat. Prawdopodobieństwa dla poszczególnych wartości węzła Transformacja PBL i węzła Zgon z powodu transformacji określono jako:
P(Transformacja PBLt = tak | Transformacja PBLt-1 = tak, Przeżyciet-1 = k) = 1, gdzie k Î {tak, nie}
P(Transformacja PBLt = tak | Transformacja PBLt-1 = nie, Przeżyciet-1= tak) = x1
P(Transformacja PBLt = tak | Transformacja PBLt-1 = nie, Przeżyciet-1 = nie) = 0
P(Zgon transformacjat = tak | Zgon transformacjat-1 = tak, Transformacja PBLt = k) = 1, gdzie k Î {tak, nie}
P(Zgon transformacjat = tak | Zgon transformacjat-1 = nie, Transformacja PBLt = tak) = x2
P(Zgon transformacjat = tak | Zgon transformacjat-1 = nie, Transformacja PBLt = nie) = 0
Z powodu obniżonej odporności u chorych z PBL często występują różnego rodzaju infekcje. Przy diagnozie ok. 15% pacjentów cierpi na infekcje o różnym podłożu a ich liczba rośnie w czasie do ok. 30% ze względu na zaawansowanie choroby, wiek pacjenta i słabą odporność. Prawdopodobieństwo wystąpienia Infekcji określono w następując sposób:
P(Infekcjet = tak | Infekcjet-1 = k, Przeżyciet-1 = tak) = xk, gdzie k Î {tak, nie}
P(Infekcjet = tak | Infekcjet-1 = tak, Przeżyciet-1 = nie) = 1
P(Infekcjet = tak | Infekcjet-1 = nie, Przeżyciet-1 = nie) = 0
Zgon z powodu infekcji jest bardzo częsty i stanowi przyczynę śmierci ok. 30% pacjentów. Prawdopodobieństwa związane z tym węzłem sieci określono w następujący sposób:
P(Zgon infekcjet = tak | Zgon infekcjet-1 = tak, Infekcjet = k) = 1, gdziek Î {tak, nie}
P(Zgon infekcjet = tak | Zgon infekcjet-1 = nie, Infekcjet = tak) = x
P(Zgon infekcjet = tak | Zgon infekcjet-1 = nie, Infekcjet = nie) = 0
Inne nowotwory również występują bardzo często u chorych na PBL. Są one diagnozowane u ok. 20% pacjentów w momencie diagnozy PBL a po 25 latach nawet połowa pacjentów może cierpieć na dodatkowe nowotwory [3]. Prawdopodobieństwa dla węzła Inne nowotwory zostało określone następująco:
P(Inne nowotworyt = tak | Inne nowotworyt-1 = k, Przeżyciet-1 = tak) = x, gdzie k Î {tak, nie}
P(Inne nowotworyt = tak | Inne nowotworyt-1 = tak, Przeżyciet-1 = nie) = 1
P(Inne nowotworyt = tak | Inne nowotworyt-1 = nie, Przeżyciet-1 = nie) = 0
Zgon z powodu dodatkowego nowotworu stwierdza się u ok. 30% pacjentów. Prawdopodobieństwa dla węzła Zgon inne nowotwory określono w następujący sposób:
P(Zgon inne nowotworyt = tak | Zgon inne nowotworyt-1 = tak, Inne nowotworyt = k) = 1, gdzie k Î {tak, nie}
P(Zgon inne nowotworyt = tak | Zgon inne nowotworyt-1 = nie, Inne nowotworyt = tak) = x
P(Zgon inne nowotworyt = tak | Zgon inne nowotworyt-1 = nie, Inne nowotworyt = nie) = 0
Część pacjentów cierpiących na PBL umiera z innych przyczyn niż wymienione powyżej, które nie są również związane z białaczką. Prawdopodobieństwo Zgonu z innych przyczyn różni się w zależności od wieku i płci pacjenta. Dla uproszczenia pacjentów podzielono na dwie grupy wiekowe (do 65 roku życia i powyżej) różnicując prawdopodobieństwo zgonu w zależności od wieku i płci w następujący sposób:
P(Zgon inne przyczynyt = tak | Zgon inne przyczynyt-1 = tak, Płećt = k, Wiekt = i) = 1, dla k Î {Mężczyzna, Kobieta}, i Î {> 65lat, <= 65 lat}
P(Zgon inne przyczynyt = tak | Zgon inne przyczynyt-1 = nie, Płećt = k, Wiekt = i) = xki dla k Î {M, K}, iÎ{> 65lat, <= 65 lat}
Prawdopodobieństwa dla węzła Zgon inne przyczyny określone wg. Dostępnych statystyk prezentuje poniższa tabela.
| Zgon inne przyczynyt-1 | Płećt | Wiekt | Zgon inne przyczynyt | |
| tak | M | >65 | tak | 1 |
| nie | M | >65 | tak | 0,0042 |
| tak | K | >65 | tak | 1 |
| nie | K | >65 | tak | 0,0028 |
| tak | M | <=65 | tak | 1 |
| nie | M | <=65 | tak | 0,00024 |
| tak | K | <=65 | tak | 1 |
| nie | K | <=65 | tak | 0,0001 |
| tak | M | >65 | nie | 0 |
| nie | M | >65 | nie | 0,9958 |
| tak | K | >65 | nie | 0 |
| nie | K | >65 | nie | 0,9972 |
| tak | M | <=65 | nie | 0 |
| nie | M | <=65 | nie | 0,99976 |
| tak | K | <=65 | nie | 0 |
| nie | K | <=65 | nie | 0,9999 |
Zgony z powodu transformacji PBL, infekcji, innych nowotworów oraz wieku i płci pacjenta wpływają na Przetrwanie chorego, które nie jest bezpośrednio związane z PBL. Prawdopodobieństwa dla węzła Przetrwanie określono w następujący sposób:
P(Przetrwaniet = tak | Przetrwaniet-1 = tak, Zgon Transformacja PBLt = nie, Zgon infekcjet = nie, Zgon inne nowotworyt = nie, Zgon inne przyczynyt = nie) = 1
P(Przetrwaniet = tak | Zgon Transformacja PBLt = k1, Zgon infekcjet-1 = k2, Zgon inne nowotworyt = k3, Zgon inne przyczynyt = k4) = 0, gdzie ki = tak dla jednego i Î {1, 2, 3, 4}
W opracowanej sieci wykorzystano klasyfikację zaawansowania choroby wg skali Rai. Węzeł Stadium PBL może przyjmować trzy wartości: stadium 0, stadium I lub II oraz stadium III lub IV. W momencie diagnozy te stadia występują w następujących proporcjach: stadium III, IV – 39% pacjentów, stadium I, II – 56% pacjentów, stadium 0 – 5% pacjentów. Część pacjentów z większym zaawansowaniem PBL (stadia I, II, III, IV) ma szansę na wyleczenie / remisję choroby w wyniku zastosowanego leczenia, co może skutkować czasową poprawą oceny stopnia zaawansowania choroby. U pozostałych pacjentów stopień zaawansowania choroby stopniowo zwiększa się, co w konsekwencji prowadzi do zgonu. Prawdopodobieństwa dla węzła Stadium PBL określono następująco:
P(Stadium PBLt = III, IV | Rokowaniet-1 = k, Stadium PBLt-1 = i, Transformacja PBLt = tak) = 1 dla kÎ{dobre, średnie, złe}, iÎ{III,IV; I,II; 0}
P(Stadium PBLt = i | Rokowaniet-1 = k, Stadium PBLt-1 = i, Transformacja PBLt = nie) = xki dla kÎ{dobre, średnie, złe}, iÎ{III,IV; I,II; 0}
Stan zdrowia pacjentów z PBL jest określany wg skali ECOG, która ma pięć stanów opisujących zdrowie chorego. Od stanu 0, gdzie pacjent jest w pełni sił fizycznych do stanu 5, który oznacza zgon chorego. Dla uproszczenia przyjęto trzy stany dla węzła Stan zdrowia: 0,1,2 – stan zdrowia dobry, 3,4 – stan zdrowia średni i 5 – zgon. Stan zdrowia jest uzależniony od stadium zaawansowania przewlekłej białaczki limfocytowej, czynników prognostycznych PBL i komplikacji związanych z chorobą, takich jak: infekcje, powikłania autoimmunologiczne. Prawdopodobieństwa wystąpienia poszczególnych wartości dla węzła Stan zdrowia określa się następująco:
P(Stan zdrowiat = dobry | Stan zdrowiat-1 = i, Rokowaniet = j, Powikłania autoimmunologicznet = k, Stadium PBLt = m, Infekcjet = k, Przetrwaniet = k) = ((((pij)k)m)k)k dla i Î {dobry, średni}, j Î {dobre, średnie, złe}, k Î {tak, nie}, m Î {III,IV; I,II; 0}
P(Stan zdrowiat = k | Stan zdrowiat-1 = zgon) = 0 dla k Î {dobry, średni}
Przeżycie pacjentów z przewlekłą białaczką limfocytową jest możliwe, gdy węzeł stan zdrowia przyjmuje wartości różne od wartości zgon:
P(Przeżyciet = tak | Stan zdrowiat ≠ zgon) = 1
W sieci zdefiniowano również węzeł Zgon, którego wartość jest przeciwieństwem wartości węzła Przeżycie, tzn.:
P(Zgont = tak | Przeżyciet = nie) = 1
P(Zgont= tak | Przeżyciet = tak) = 0
Prawdopodobieństwa węzłów, gdy wiadomo, że np. liczba zgonów pacjentów z powodu infekcji na przestrzeni 25 lat to ok. 30%, należało określić dla pojedynczego kroku czasowego w sieci dynamicznej (6 miesięcy). Te wyliczenia przeprowadzono na podstawie wzoru wykorzystanego w pracy M. Van Gerven, B. Taal [4]:
Gdzie Pm jest szukanym prawdopodobieństwem dla pojedynczego kroku czasu m, n jest krokiem czasu, w którym znamy prawdopodobieństwo Pn. W przypadku zgonu ze względu na infekcje n=300, m=6 a Pn=0,3. Szukane prawdopodobieństwo dla pojedynczego kroku m wynosi 0,007.
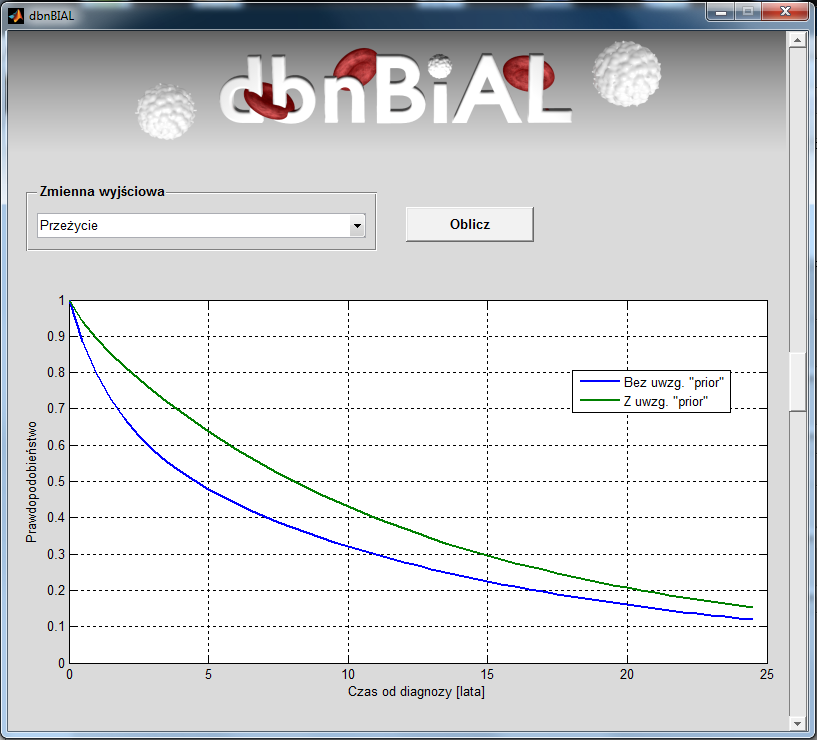
Poniżej przedstawiono wynik przykładowej symulacji dla pacjenta będącego mężczyzną w stadium zaawansowania 0, i wieku powyżej 65 lat w chwili rozpoznania PBL.
Linki:
- Wersję instalacyjną aplikacji dla systemu operacyjnego MS Windows można pobrać z następującej lokalizacji: http://dbnbial.ibib.waw.pl/MyAppInstaller_dbnBIAL.exe
Referencje:
1. F. Van Bockstaele, B. Verhasselt, J. Philippe – Prognostic markers in chronic lymphocytic leukemia: A comprehensive review. Elsevier. Blood Reviews (2009) 23, 25-47.
2. G. Dighiero, T. J. Hamblin – Chronic lymphocytic leukemia. Lancet 2008; 371: 1017-29.
3. Przewlekła białaczka limfatyczna. Czas na zmianę standardów postępowania? – Andrzej Deptała, wykład – http://tip.wum.edu.pl/files/tip/Przewlekla_bialaczka_limfatyczna.pdf
4. M. van Gerven, B. Taal – Structure and parameters of a Bayesian network for carcinoid prognosis.

 Polski
Polski English
English