metaBIAL

metaBIAL – symulator działający on-line, umożliwiający porównywanie skuteczności stosowania różnych opcji chemioterapii i immunoterapii jako pierwszej linii leczenia u pacjentów z przewlekłą białaczką limfocytową B-komórkową w odniesieniu do czasu przeżycia bez progresji choroby oraz całkowitego czasu przeżycia.

Opis & Grafika

Obecnie dostępnych jest wiele opcji leczenia pacjentów chorych na progresywną, objawową przewlekłą białaczkę limfocytową (PBL) opartych na zastosowaniu leków alkilujących (np. chlorambucyl, bendamustyna), analogów puryn (np. fludarabina) lub przeciwciał monoklonalnych (np. alemtuzumab, rituximab) w formie monoterapii bądź w różnych kombinacjach. Skuteczność kilku z tych schematów leczenia u pacjentów z wcześniej nieleczoną PBL porównywano wcześniej bezpośrednio w trakcie badań klinicznych z losowo dobieranymi grupami pacjentów (ang. Randomized controlled trial – RCT) w odniesieniu do czasu przeżycia bez progresji choroby (ang. progression free survival – PFS) oraz w odniesieniu do całkowitego czasu przeżycia (ang. Overall survival – OS). Jednak dostępne dane na ten temat są ograniczone a większość schematów leczenia nie była dotychczas bezpośrednio porównywana.

Celem opracowania symulatora metaBIAL było stworzenie możliwości porównywania efektywności różnych schematów leczenia pacjentów z wcześniej nieleczoną PBL w odniesieniu do PFS i OS. Przebiegi krzywych przeżycia, przewidywane z użyciem symulatora metaBIAL, bazują na modelach ryzyka dla poszczególnych opcji leczenia, wykorzystujących metodę wielomianów cząstkowych pierwszego i drugiego stopnia. Modele stosowane w symulatorze metaBIAL zostały wyselekcjonowane spośród szerokiej grupy parametrycznych funkcji przeżycia, obejmującej m.in. kilka popularnych i często stosowanych modeli, takich jak model Weibulla czy model Gompertza a zastosowana metoda nie wymuszała czynienia założeń co do stałości ilorazu ryzyka dla poszczególnych porównywanych opcji leczenia.

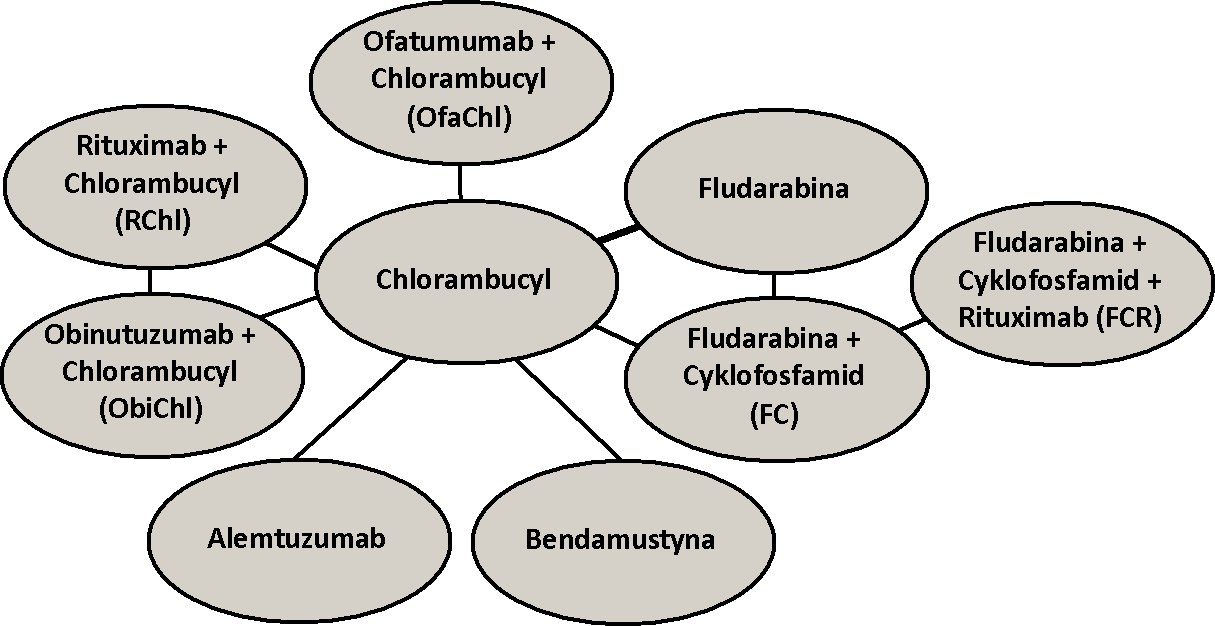
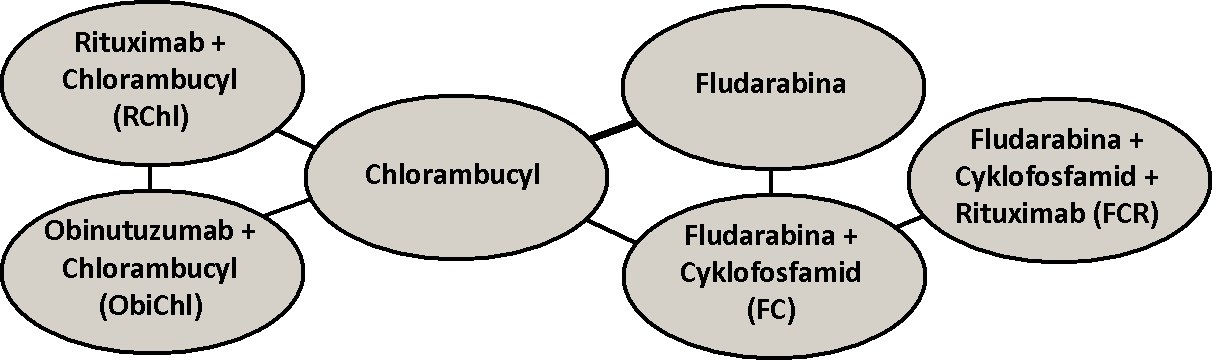
Modele użyte w symulatorze metaBIAL wybrano na podstawie analizy wyników badań RCT przeprowadzonych przez innych badaczy i opisanych w literaturze. Systematyczny przegląd literatury przeprowadzono na podstawie materiałów źródłowych dostępnych w bazach NCBI PubMed oraz Cochrane Library. Poszukiwano badań RCT, których wyniki opublikowano w języku angielskim przed styczniem 2014 r. Przeprowadzona kwerenda miała na celu zidentyfikowanie raportów z badań zawierających nazwy leków stosowanych w pierwszej linii leczenia PBL (leki te zidentyfikowano na podstawie National Comprehensive Cancer Network (NCCN) Clinical Practice Guidelines) lub słowa kluczowe takie jak: „CLL”, „drugs” oraz „treatment”. Następnie przeanalizowano spisy piśmiennictwa w zidentyfikowanych publikacjach, aby odszukać ewentualne dodatkowe raporty spełniające warunki włączenia do prowadzonej analizy. W rezultacie zidentyfikowano 467 raportów z badań, które zawierały poszukiwane słowa kluczowe, bądź były uwzględnione w spisach piśmiennictwa takich raportów. Następnie przeanalizowano tytuły i abstrakty zidentyfikowanych raportów, aby wyeliminować z dalszej analizy te z nich, które opisywały zastosowanie tylko jednego schematu leczenia, nie opisywały wyników RCT lub dotyczyły drugiej i dalszych linii leczenia. W ostatnim etapie badania literatury, na podstawie analizy głównych tekstów publikacji wybranych we wcześniejszych etapach, wybrano te raporty, które dotyczyły PFS oraz OS i, w których autorzy przedstawili wykresy tych parametrów a pod wykresami umieścili informację na temat liczby pacjentów w poszczególnych okresach obserwacji. Ostatecznie do analizy włączono wyniki 9. badań RCT [1-9], w których analizowano PFS oraz wyniki 6. badań [1-6], w których analizie podlegał parametr OS. Sieci badań, które użyto do określenia modeli ryzyka, dotyczących odpowiednio parametru PFS oraz OS, przedstawiono na poniższych rysunkach.

W symulatorze metaBIAL zastosowano podejście oparte na wielowymiarowej analizie wyniku leczenia. Podejście to stanowi rozszerzenie meta-analizy sieciowej, w której efekt leczenia jest reprezentowany przez pojedynczy parametr [10]. Modele ryzyka dla poszczególnych opcji leczenia opisano kilkoma parametrami z wykorzystaniem wielomianów cząstkowych pierwszego lub drugiego rzędu. W podejściu tym, w najprostszym przypadku, tzn. w przypadku zastosowania wielomianu pierwszego rzędu, logarytm ryzyka (hAt) leczenia A w chwili t opisany jest zależnością [10]:

ln(h_At) = b_0A + b_1A t^p   gdzie t⁰ = log(t)

Jeżeli wielomian pierwszego rzędu zostanie użyty dla pojedynczego badania RCT porównującego dwie opcje leczenia (A i B), wówczas parametry modelu dla leczenia B można zapisać jako:

b_0B = b_0A + d₀ and b_1B = b_1A + d₁

gdzie wektor (d₀ d₁) opisuje różnicę parametrów b₀ and b₁ dla logarytmu ryzyka leczenia B względem leczenia A.

Modele stosowane w meta-analizie do bezpośredniego porównania leczenia B z leczenie A można uogólnić tak, by możliwe było równoczesne porównywanie leczenia B vs A i C vs A. Warunkiem koniecznym uzyskania miarodajnych rezultatów w wyniku takiej meta-analizy jest porównywalność poszczególnych badań RCT z punktu widzenia zmiennych towarzyszących, wpływających na względny efekt analizowanych opcji leczenia. Jeśli warunek ten jest spełniony, możliwe jest skonstruowanie sieci badań RCT posiadających wspólne „ramiona” i przeprowadzenie bezpośrednich i pośrednich porównań poszczególnych opcji leczenia z zachowaniem wysokiej mocy takiej analizy, wynikającej z losowego doboru pacjentów. W przypadku tego typu meta-analizy sieciowej dotyczącej zmiennej dwuwartościowej, efekt leczenia C vs B, tj. d_BC, można obliczyć na podstawie bezpośrednich efektów A vs B i C vs A z użyciem następującego równania:

d_BC = d_AC – d_AB

Gdy analiza dotyczy przeżycia, porównanie różnych opcji leczenia odbywa się z wykorzystaniem logarytmów ilorazu ryzyka (HR) a zaprezentowane poniżej równanie stosuje się dla każdej chwili czasowej t:

ln(HR_BC(t)) = ln(HR_AC(t)) – ln(HR_AB(t))

HR_BC(t) odzwierciedla iloraz ryzyka związanego z leczeniem C względem B w chwili t. W związku z tym, w zastosowanym modelu ryzyka bazującym na wielomianach cząstkowych, różnice w wartościach parametrów modelu b₀ i b₁ są niezależne od czasu i np. dla porównania B vs C mogą być one opisane z wykorzystaniem różnic b₀ i b₁ dla porównania A vs C i A vs B. Meta-analiza sieciowa może więc być przeprowadzona z wykorzystaniem różnic parametrów b₀ and b₁ dla zmian logarytmu ryzyka między poszczególnymi badaniami. Stosując różne wartości p możliwe jest przetestowanie szerokiego zakresu kształtów krzywych opisujących logarytm ryzyka i w konsekwencji wybranie takiego modelu ryzyka, który najlepiej oddaje dane eksperymentalne oraz użycie go do przeprowadzenia analizy przeżywalności.

W celu dobrania najlepszego modelu ryzyka analizę rozpoczęto od zdygitalizowania krzywych przeżycia (odpowiednio PFS i OS) przedstawionych w poszczególnych badaniach RCT. Zeskanowane krzywe Kaplana-Meiera zostały podzielone na 2-miesięczne interwały (Δt) przez całe okresy obserwacji stosowane w poszczególnych badaniach RCT. Dane zostały skorygowane, w celu uwzględnienia uciętych danych (ang. cenzored), zgodnie z metodą zaproponowaną przez Jensena [10]. W każdym przedziale czasu [t, t+Δt] w każdym badaniu j i dla każdej opcji leczenia k, określono liczbę pacjentów na początku wspomnianego przedziału czasu (n_jkt) oraz liczbę pacjentów, która w tym przedziale czasu doświadczyła zdarzenia zgodnego z definicją PFS, tj. progresja choroby lub zgon lub OS, tj. zgon (r_jkt).

Do opisu wartości r_jkt na podstawie n_jkt i prawdopodobieństwa zajścia zdarzenia zgodnego z definicją PFS lub OS w każdym przedziale [t, t+Δt] zastosowano rozkłady dwumianowe:

r_jkt ∼ bin(p_jkt, n_jkt)

Ryzyko uznawano za stałe w danym przedziale czasu i obliczano je z zastosowaniem następującej zależności:

h_jkt = −ln(1 – p_jkt)/Δt

Najlepszy model ryzyka wybrano na podstawie wyników analizy modeli wykorzystujących wielomiany cząstkowe pierwszego i drugiego rzędu z wykładnikami z następującego zakresu wartości: -2, -1, -0,5, 0, 0,5, 1, 2 oraz 3. Obliczenia przeprowadzono zarówno dla modeli o efektach stałych jak i dla modeli o efektach losowych. W tym drugim przypadku, uwzględniono heterogeniczność obydwu parametrów d₀ and d₁.

Sieć badań RCT obejmowała dwa badania [3, 6] złożone z trzech ramion (porównujące po 3 opcje leczenia) a zastosowany model o efektach losowych nie uwzględniał poprawki związanej z korelacją wyników dla badań zawierających więcej niż dwa ramiona. W celu zminimalizowania potencjalnego wpływu tych korelacji na wyniki analizy, każde z badań zawierających trzy ramiona podzielono na dwa badania o dwóch ramionach dzieląc jednocześnie pomiędzy te badania pacjentów podlegających leczeniu przyjętemu za bazowe [11].

Przyjęto nieinformacyjne dwuwymiarowe rozkłady normalne a priori opisujące średnie wartości parametrów dla opcji leczenia przyjętych w poszczególnych badaniach RCT jako bazowe. Podobne rozkłady a priori przyjęto odnośnie różnic parametrów dla poszczególnych opcji leczenia względem leczenia bazowego w każdym badaniu. Dla wariancji różnic efektów leczenia przyjęto nieinformacyjny rozkład Wisharta.

Parametry poszczególnych modeli estymowano z użyciem metody Monte Carlo łańcuchów Markowa (MCMC) za pomocą systemu OpenBUGS 3.2.1 (http://www.openbugs.info/w/) [12]. Obliczenia prowadzono z użyciem czterech łańcuchów. Wyniki pierwszych 10.000 iteracji z „thining’iem” równym 10 odrzucano jako „burn-in” a wyniki kolejnych 25.000 iteracji używano do wnioskowania. Zbieżność uzyskanych wyników potwierdzano z zastosowaniem kryterium Gelmana-Rubina. Sprawdzano również autokorelacje wyników oraz błąd Monte-Carlo.

Wyboru najlepszego modelu hazardu dokonywano na podstawie wartości DIC (ang. deviance information criteria), którą traktowano jako miarę jakości dopasowania wyników generowanych przez model do danych eksperymentalnych z uwzględnieniem stopnia złożoności modelu [13]. Modele, które uzyskiwały najniższą wartość DIC, tj. opisywały najdokładniej dane eksperymentalne, zastosowano do obliczenia zmian ryzyka, ilorazów ryzyka oraz przeżycia (odpowiednio PFS i OS) w czasie dla poszczególnych opcji leczenia PBL.

Dla PFS najlepszym modelem okazał się model z efektem losowym i wykładnikiem p równym –0,5. W przypadku badań obejmujących młodszych pacjentów znajdujących się w lepszej formie fizycznej najlepszym modelem był model z wykładnikiem p równym –2. Natomiast w grupie badań obejmujących starszych pacjentów w gorszej kondycji – najlepszym modelem był model Weibulla z wykładnikiem równym zero, co oznacza, że logarytm ryzyka był proporcjonalny do log(t).

Stwierdzono, że model ze stałym efektem, opisujący ln(h) wielomianem cząstkowym pierwszego rzędu z wykładnikiem równym 2, był najlepiej dopasowany do danych eksperymentalnych dotyczących OS zarówno dla sieci złożonej ze wszystkich badań, jak i dla sieci grupujących badania dotyczące młodszych pacjentów w lepszej kondycji, jak i starszych w gorszej kondycji fizycznej.

Szczegóły przeprowadzonych analiz opisano w innym miejscu [14].

Linki:

• http://metabial.ibib.waw.pl

Referencje:

1. Rai KR, Peterson BL, Appelbaum FR, et al. Fludarabine compared with chlorambucil as primary therapy for chronic lymphocytic leukemia. N Engl J Med 2000;343:1750–7.
2. Eichhorst BF, Busch R, Hopfinger G., et al. Fludarabine plus cyclophosphamide versus fludarabine alone in first-line therapy of younger patients with chronic lymphocytic leukemia. Blood 2006;107:885–91.
3. Catovsky D, Richards S, Matutes E, et al. Assessment of fludarabine plus cyclophosphamide for patients with chronic lymphocytic leukaemia (the LRF CLL4 Trial): a randomized controlled trial. Lancet 2007;370:230–9.
4. Eichhorst BF, Busch R, Stilgenbauer S, et al. First-line therapy with fludarabine compared with chlorambucil does not result in a major benefit for elderly patients with advanced chronic lymphocytic leukemia. Blood 2009;114:3382–91.
5. Hallek M, Fischer K, Fingerle-Rowson G, et al. Addition of rituximab to fludarabine and cyclophosphamide in patients with chronic lymphocytic leukaemia: a randomize, open-label, phase 3 trial. Lancet 2010;376:1164–74.
6. Goede V, Fischer K, Busch R, et al. Obinutuzumab plus chlorambucil in patients with CLL and coexisting conditions. New Eng J Med 2014;370: 1101–10.
7. Hillmen P, Skotnicki AB, Robak T, et al. Alemtuzumab compared with chlorambucil as first-line therapy for chronic lymphocytic leukemia. J Clin Oncol 2007;25:5616–23.
8. Knauf WU, Lissitchkov T, Aldaoud A, et al. Bendamustine compared with chlorambucil in previously untreated patients with chronic lymphocytic leukaemia: updated results of a randomized phase III trial. Brit J Haematol 2012;159:67–77.
9. Hillmen P, Robak T, Janssens A, et al. Ofatumumab + chlorambucil versus chlorambucil alone in patients with untreated chronic lymphocytic leukemia (CLL) Results of the Phase III Study COMPLEMENT 1 (OMB110911). Blood 2013;122: Abstract 528.
10. Jansen JP. Network meta-analysis of survival data with fractional polynomials. BMC Med Res Methodol 2011;11:61.
11. Higgins JPT, Green S (editors). Cochrane Handbook for Systematic Reviews of Interventions Version 5.1.0 [updated March 2011]. The Cochrane Collaboration, 2011. Available from www.cochrane-handbook.org, last accessed on February 15^th, 2014.
12. Lunn D, Spiegelhalter D, Thomas A, Best N. The BUGS project: Evolution, critique and future directions (with discussion). Stat Med 2009;28:3049–82.
13. Spiegelhalter DJ, Best NG, Carlin BP, van der Linde A: Bayesian measures of model complexity and fit. J Royal Stat Soc, Series B 2002;64:583-639.
14. Ladyzynski P, Molik M, Foltynski P: A network meta-analysis of progression free survival and overall survival in first-line treatment of chronic lymphocytic leukemia. Cancer Treat Rev, 2015 41(2):77-93.