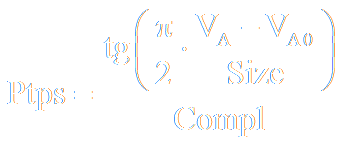BIOCENTRUM OCHOTA INFRASTRUKTURA INFORMATYCZNA DLA ROZWOJU STRATEGICZNYCH KIERUNKÓW BIOLOGII I MEDYCYNY

VirRespir

The idea of the project

There are several models of the respiratory system (RS) but usually at least one of sets of physiological phenomena are simulated only approximately or
they are not simulated at all. For example, the following may be ignored:

influence of gravity or other factors on ventilation and perfusion distribution,
such description of airways that enables to simulate accurately airflow during both weak (tidal-breathing) and forced inspiration and expiration (forced spirometry) as well as all intermediate ways of breathing or artificial ventilation in health and diseases,
transfer of gas species in airways and their transport with blood, gas exchange in lungs, and oxygen consumption in tissues,
high nonlinearities in the pulmonary circulation and its dependence on several factors such as perivessel oxygen tension, for example, etc.

Certainly, simple models can be useful in particular applications defined priori to model development. If, however, a model is intended to be used in applications not known before model development, it has to take into account as many factors and phenomena as possible. In particular, if a model is developed for other researchers, for education, or for new medical equipment testing, it has to reflect the real RS as fully as possible. Indeed, we cannot know future investigations of the others, we cannot know students’ ‘invention’, we usually cannot know a priori all features of RS which are important in case of a new equipment test (e.g. Golczewski T, Palko KJ. Biocybern Biomed Eng 2013; 33:136-144).

Authors of models of the cardiovascular system, i.e. the heart and systemic circulation, usually use extremely simple models of RS to supply those models with pulmonary blood flows and pressures as well as saturations. This may be caused by the fact that specialists in the cardiovascular system usually are not specialists in pulmonary physiology.

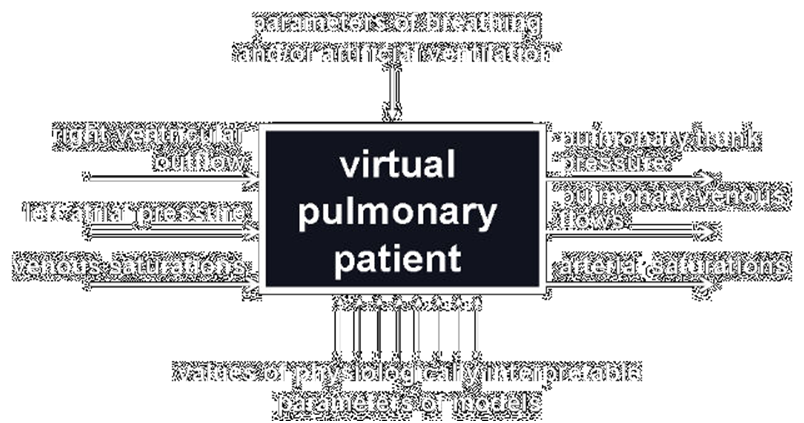
Our virtual pulmonary patient as a white box.

Taking the above into account, the aim of this project is to prepare our model as a white box available through Internet to enable other scientists and lectors to use it as a supplement to their models of the cardiovascular system or as the stand-alone model in research or education, esp. e-learning.

This white box has three variables as the input and three other variables as the output. It can be connected with all models of cardiovascular system having corresponding outputs and inputs. Breathing parameters can be adjusted manually or as a function of arterial blood saturations. Values of physiologically interpretable parameters of the box can be changed as a percentage of some standard values. If a user has not any own model of the cardiovascular system, a simple model will supply the white box inputs.

Artificial cardio-pulmonary patient

The idea of our artificial patient

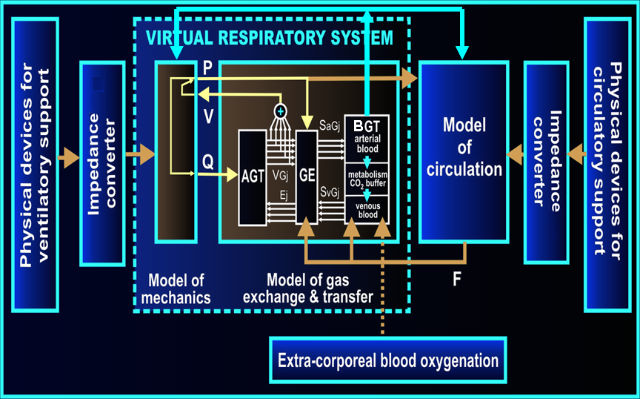
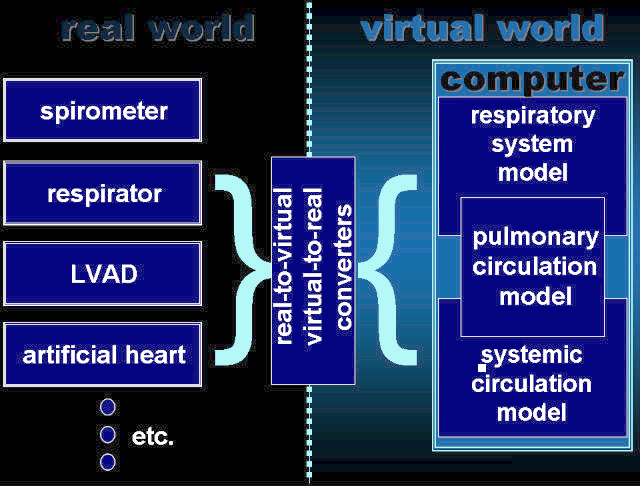
Our artificial cardiopulmonary patient is a set of several computer models cooperating one another, which may contact with real world, e.g. medical equipment, by means of our virtual-to-real converters. According to an individual application, the computer part of the artificial patient may consist of one or more of the following models:

a model of RS mechanics,
a model of pulmonary circulation,
one of models of systemic circulation developed in cooperation with Istituto di Fisiologia Clinica (Italy),
a model of gas transfer and exchange,
some additional models of physiological aspects such as breathing control based on oxygen and carbon dioxide tensions in the arterial blood or baroreflex (developed in cooperation with Istituto di Fisiologia Clinica, Italy),
models of medical equipments if initial investigations do not require tests of real equipments.

The general architecture of our artificial patient: AGT- airway gas transfer module, GE- gas exchange module, BGT- blood gas transport module, P- pressures, V- volumes, Q- airflows, F- blood flows, SaG, SvG – oxygen and carbon dioxide saturations of arterial and venous blood, respectively. Impedance converter – technical realization of virtual-to-real converters.

Some details of the models

Distributed-parameter elements

Tubes that are both significantly compliant and resistive, such as pulmonary capillaries and bronchi of middle orders, have to be represented by a distributed-parameter model. Indeed, if a fluid flows in a tube, the transmural pressure that determine the cross-section area of the tube because of compliance decreases along the tube because of resistance. Thus, the cross-section area decreases along the tube, which increases the resistance, which additionally decreases the transmural pressure and cross-section area along the tube, and so on; thus, equations describing the flow have to contain derivative with respect to a variable representing the place of a tube.

On the other hand, however, distributed-parameter models are time-consuming while models being numerical parts of an artificial patient have to work quickly, in the real time, since this patient contacts with the real world.

For those reasons, although pulmonary capillaries and bronchi of middle orders are described mathematically as distributed-parameter elements, they are described in such a way that differential equations can be solved manually, and not these equations but their solutions are used in the computer realization as lumped-parameter elements.

Thus, the models are partly distributed-parameter models from the mathematical point of view but they are lumped-parameter models from the computer realization point of view.

Physiological interpretability

Since the artificial/virtual patient is intended to be used also by physicians, parameters that physicians can change have to have physiological or medical meaning. Therefore, equations have to have an interpretable forms even if those forms do not reflect physiological phenomena so accurately as more correct but not interpretable ones. The dependence of the recoil pressure on the lungs volume can be an example. Although this dependence is usually described with an exponential function, the following function is used in the model of RS mechanics:

where:

Size − the parameter which may be treated as the size of lungs, i.e. the amount of parenchyma; for example: the Size value depends on patient’s height, and resection of a lung part results in a corresponding decrease of the Size value,
Compl − the parameter that describes compliant properties of the lung parenchyma; it can be treated as the parenchyma unitary compliance,
VA0 − the internal volume of dissected lungs, i.e. the volume when the recoil pressure is equal to zero.

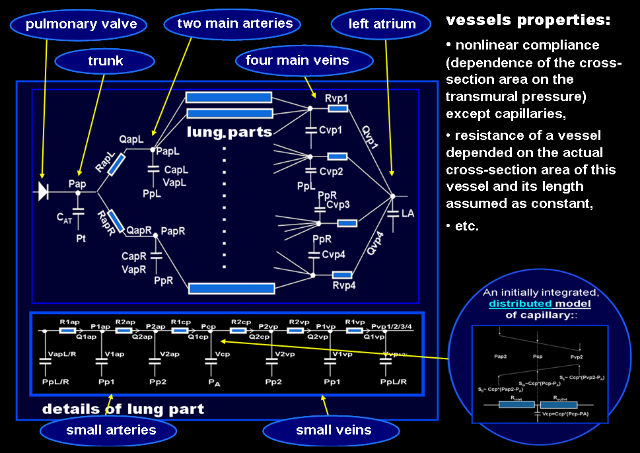
Lungs partition

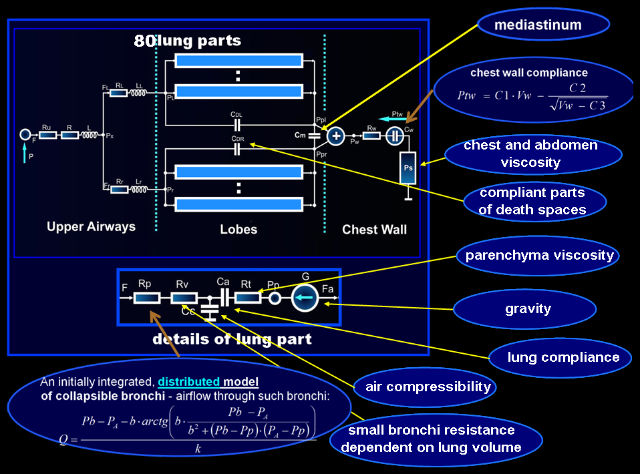
Ventilation, perfusion, and gas exchange may be different in different parts of lungs because of gravity influence, inhomogeneity of properties, asymmetrical work, etc. To make it possible to simulate such differences, lungs were divided into 80 parts, i.e. divided anatomically into 5 lobes and each lobe was divided geometrically into 16 parts by means of three horizontal planes (influence of gravity in the vertical position of the patient) and two vertical planes mutually orthogonal (influence of gravity in the supine and lateral positions).

The model of respiratory system mechanics

The features of the mechanics described below are taken into account, among others, to enable a user to simulate a range of problems as wide as possible.

According to mechanical and physiological differences between bronchi of different order, the airways resistances are divided into:

lumped resistances of the large bronchi and upper airways – they are described with a quadratic equation where the linear coefficient represents the Ohm’s resistance and the quadratic coefficient may be related to both turbulent flow and Bernoulli’s principle;
resistances that depend on the transmural pressure, i.e. the resistances of bronchi of higher order that may collapse causing airflow limitation – they are represented by equations describing the relationship between the airflows and pleural, alveolar, and upper airways pressures;
lumped resistances that depend directly on the lung volume, i.e. the resistances of the smallest and short bronchi and ducts that are a component of the lung parenchyma – they are described with a homographic function of the lung part volume;

Note that anatomical properties of the collapsing bronchi make it necessary to treat those bronchi as both significantly resistive and compliant tubes. In such a tube, a pressure drop caused by airflow along this (resistive) tube results in a decreases of the local transmural pressure, which modifies the local cross-section area of this (compliant) tube. On the other hand, changes in the local cross-section area causes local resistance alteration, which modifies the pressure drop. As it has been noted above, such significantly compliant and resistive tubes as those bronchi and pulmonary capillaries (see below) have to be treated as distributed parameter elements. However, if properties of such a tube are described mathematically with a differential equation that can be manually integrated, the tube can be treated in a model as a lumped parameter element described by means of the solution of this differential equation.

The lungs and chest are separated and both lungs are considered independently which, for example, makes it possible:

to consider separately the chest wall and lungs compliances and their nonlinearity,
to determine the intrapleural pressure which is one of the most important quantities as, for example, it is important in ventilation analysis as well as in forced spirometry and cardiovascular system work simulations,
to divide the lungs into five lobes (and then each lobe into smaller parts) which enables to simulate and analysis such important feature and phenomena as the ventilation to perfusion ratio and influence of gravity,
to take into account non-homogeneity of lungs and influence of mediastinum properties on the RS mechanics.

Air compressibility in lungs is also taken into account. It is often neglected in models of RS mechanics, where volumes are not present and pressures in compliant elements are connected directly with airflows by means of integrations. However, since amounts of gas species are essential for gas exchange and transfer, the volumes of lung parts have to be present in a model of mechanics that cooperates with a model of gas exchange. Additionally, the volumes of lungs (their parts) are necessary when nonlinearity of the parenchyma and chest wall compliances as well as the mediastinum are taken into account. As these volumes cannot reflect the gas amount precisely because the amount depends also on the alveolar pressure, additional compliant capacitors are introduced: they store the differences between the real gas amount in lung parts and the amount that would be in these parts at the atmospheric pressure treated as the reference pressure. Note, for example, that only when air compressibility is taken into account, the volume of a lung part may decrease during expiration when there is no airflow because of bronchi closure.

The model of pulmonary circulation

The pulmonary circulation model consists of the pulmonary trunk, two main pulmonary arteries, four pulmonary veins, and smaller vessels in parts of lungs divided in the way explained in the respiratory mechanics model description.

As pulmonary vessels are very compliant, and thus their actual mechanical properties depend significantly on the transmural pressure and cross-section area, the big vessels are characterized by nonlinear compliances as well as by nonlinear and changeable resistances depended on the squared volumes of blood in these vessels.

Circulatory system in each part of lungs is represented by a proximal artery, distal one, capillary, distal vein, and proximal vein connected in series. Resistance and compliance of these small vessels, except capillaries, are described like big vessels. As pulmonary capillaries are both compliant and significantly resistive in comparison with the other pulmonary vessels, they were modeled as described above, i.e. mathematically as distributed parameter elements but in computer realization as lumped parameter elements.

The model of gas transfer and exchange

The gas transfer and exchange model consists of the following three modules:

an airway gas transfer module which calculates mixing and transfer of gas species in airways to/from lungs parts ; it uses airflows supplied by the RS mechanics model,
a gas exchange module which determines passage of gas species from/to lungs to/from blood in pulmonary capillaries; it uses pressures supplied by the model of RS mechanics and blood flows provided by the model of pulmonary circulation,
a blood gas transport module which calculates transport of gas species with blood to/from tissues as well as it describes oxygen consumption and carbon dioxide production; it uses blood volumes and flows provided by the pulmonary circulation and CV models.

Four possible gas species are considered in the model: O2, CO2, nitrogen, and some other species, e.g. an anesthetic. In the airway gas transfer module also saturated water vapor is taken into account. Since the partial pressure of the saturated vapor is constant (at constant body temperature), the vapor quantum in lungs parts depends on the lungs parts volumes only. The other gas species can be compressed, and thus their amounts depend on both their partial pressures and lungs parts volumes.

From the point of view of the airway gas transfer module, the RS consists of lungs parts and the anatomical dead space which is divided into the trachea (or an intratracheal tube if it is used), main bronchi, and the remaining parts of the left and right anatomical dead spaces corresponding to compliant dead spaces in the model of RS mechanics. Each of these airway elements is divided into several segments to make it possible to simulate different concentrations of various gas species in different points of airways. Such division is especially important for correct simulation of dead space ventilation and its influence on alveolar gas species concentrations. lungs parts are treated as single segments since if a portion of a gas species flows into an alveolus, it can be assumed to be present immediately in the whole volume of this alveolus because alveoli are very small (such microscopic phenomena as diffusion screening were neglected).

Transfer of each gas species from a segment of the RS to one or more neighboring ones is proportional to its concentration in this segment and to the airflows. In the case of lung parts, the transfer is supplemented with a particular gas species exchange. Although gas transfer with diffusion is not simulated directly, it is present because of the finite volumes of the segments (a species portion that flows into a segment “diffuses” immediately into the whole segment volume).

It has been assumed that blood flowing through lung capillaries has enough time to be saturated maximally. This means that end-capillary tensions are equal to alveolar partial pressures for all four gas species. This assumption is usually accurate except in such cases as very extreme exercise (blood flows too quickly) or a diffusion disturbance (gas exchange needs much more time). The end-capillary blood concentrations of gas species in individual lungs parts are calculated using the alveolar partial pressures of these species in lungs parts and: slightly modified Hill’s equation for O2, a power equation with the exponent smaller than 1 for CO2, and proportionality for nitrogen (the fourth species has not been utilized yet). Gas exchange, i.e. the gas species quantum that flows from alveolar space of an individual lungs part into the blood is proportional to the rate of blood flow through capillary of that lungs part and the difference between the calculated end-capillary concentrations and mixed venous blood concentration.

Blood saturated differently in individual lungs parts is mixed in LA where the final arterial blood concentrations are determined. In the simple embedded model of the systemic circulation, such homogenously saturated arterial blood flows through the aorta and arteries to capillaries in tissues. CO2 production depends on O2 consumption and respiratory quotient RQ, however, only small part of the CO2 produced (about 10%) is transferred directly to the blood; although the rest is stored in different CO2 buffers with different properties, only one resultant buffer is assumed in the blood gas transport module. The rate of CO2 transfer from the buffer to the blood is proportional to the difference between CO2 tensions in the buffer and blood.

Links:

VirRespir

References:

Bio-Med

Portal współfinansowany jest ze środków Europejskiego Funduszu Rozwoju Regionalnego w ramach Programu Operacyjnego Innowacyjna Gospodarka, projekt: Biocentrum Ochota - infrastruktura informatyczna dla rozwoju strategicznych kierunków biologii i medycyny (nr : POIG.02.03.00-00-003/09)